Suurten lukujen laki ja talon etu
Mitä pidempään pelaat, sitä varmemmin ja sitä enemmän jäät häviölle aina, kun palautusprosentti on alle sata.
Mitä enemmän rahapelejä pelaat, sitä varmemmin jäät tappiolle
Suurten lukujen laki rahapeleihin sovellettuna tarkoittaa, että mitä useamman kierroksen satunnaista peliä pelaa, sitä lähemmäksi pelin palautusprosenttia tai pelinjärjestäjän näkökulmasta ns. talon etua tulos asettuu.
Ihmisillä on taipumus tehdä lyhyistä sarjoista ennustuksia ja ajatella, että satunnaisuus on reilu ja se korjautuu nopeasti.
Lue myös Satunnaisuus ja tapahtumien riippumattomuus
Noppaesimerkki
Symmetristä noppaa 1000 kertaa heitettäessä jokaista silmälukua tulee todennäköisesti yhtä monta kertaa. 10 000 kertaa heitettäessä jakauma on entistä tarkempi jokaiselle silmäluvulle.
Jos palautusprosentti olisi 100, sinun pitäisi saada kuusinkertainen voitto panokseesi nähden yksittäistä silmälukua arvatessasi (nopassa on 6 sivua eli tässä tapauksessa 6 mahdollisuutta). Tällöin jäisit pitkään pelatessasi todennäköisesti suurin piirtein nollille.
Talon etu
Koska pelinjärjestäjän ei kannata tällaista peliä järjestää, voittokerroin olisi oikeassa pelissä alhaisempi kuin 6. Pelinjärjestäjä järjestää siis palautuksen sellaiseksi, että se saa itselleen niin sanotun talon edun. Talon edun vuoksi saatkin tässä esimerkissä kuusinkertaisen voiton sijaan vain viisinkertaisen voiton.
- Onnistumismahdollisuudet veikata oikein on 1/6 kun sinulle maksetaan voittoa 5/1. Palautusprosentti yksittäiselle heitolle on siis 5/6 = 0,83 -> 83 %
Ravintolaruletissa on lähes sama voittosuhde, kun panostetaan yksittäiseen numeroruutuun (83,6 %): Onnistumismahdollisuutesi on 1/37, kun voiton osuessa sinulle maksetaan 30/1. (Värille ja muille sivusektoreille palautusprosentti on korkeampi).
- Jos heittäisit noppaa 1200/2400 kertaa 1 e:n panoksella per kierros, todennäköisesti veikkaisit silmäluvun oikein keskimäärin kerran kuudesta, eli noin 200/400 kertaa.
Jos palautus olisi 100% (voitto 6 x panos)
- 1200 keraa: Panostaisit 1200 e ja voitaisit n. 1200 e -> jäisit suurin piirtein nollille.
Kun palautus on 83 % (voitto 5 x panos)
- 1200 kertaa: Panostaisit 1200 e ja voittaisit n. 1000 e -> jäisit (suurin piirtein) 200 e häviölle
- 2400 kertaa: panostaisi 2400 e ja voittaisit n. 2000 e -> jäisit (suurin piirtein) 400 e häviölle.
Jos jatkat pelaamista jäljelle jääneellä rahalla, pelikassasi kuihtuu jokaisella kierroksella 17 %, kunnes se loppuu:
2000 e -> 1660 e -> 1377 e …
1000 e -> 830 e -> 689 e …
Yksittäistä nopan heittoa on mahdotonta ennustaa. Tuhannenkin nopan heiton sisään mahtuu useita sarjoja, joissa samaa silmälukua tulee useampi kerta putkeen.
Esimerkki ruletista
Helposti voisi esimerkiksi kuvitella, että ruletissa näiden viiden värin sarjojen esiintymisen todennäköisyys vaihtelisi:
- P-M-P-M-P
- P-P-P-P-P
- M-M-P-M-M
(P=punainen, M=musta)
Kaikkien näiden sarjojen esiintymisen todennäköisyys on kuitenkin täsmälleen sama -> (18/37)5 = 2,7 %.
Ei ole siis mitään väliä, kumpaa väriä arvaat: todennäköisyys on aina sama. Jo hetken ruletin voittotaulukkoa katsellessaan alkaa helposti nähdä mitä eriskummallisemmilta näyttäviä sarjoja: ihmisen mieli alkaa muodostaa sarjoista säännönmukaisuuksia. Tällöin on hyvä muistuttaa itseään pelien luonteesta pitkällä aikavälillä.
Taloa vastaan pelattavissa kiinteäkertoimisissa peleissä (kaikki kasinopelit, peliautomaatit yms.) ei ole mahdollista pitkällä aikavälillä jäädä edes omilleen, ellei mieletön tuuri tuo pelaajalle yksittäistä todella suurta voittoa. Tämän varaan ei kannata laskea. Pitkää aikaväliä voi siis ennustaa, lyhyttä ei.
Tämä on suurten lukujen lain periaate: Talon edun vuoksi mitä enemmän rahapelejä pelaat, sitä varmemmin jäät tappiolle.
Neljä kierrosta ruletin väriä - miten käy?
Ruletissa punaisen tai mustan esiintymisen todennäköisyys on jokaisella kerralla ko. värien määrä / kaikkien numeroiden määrä.
- Mustia numeroita on 18, punaisia on 18 ja vihreitä numeroita on 1 (numero nolla). Yhteensä numeroita on siis 37, joten todennäköisyys mustalle/punaiselle on 18/37 = 48,6 %
- Todennäköisyys, että arvaat värin väärin on yksittäisellä kerralla siis 51,4 %.
Talon etu näyttää yksittäisellä kierroksella pieneltä. Pidempään pelatessa todennäköisyydet alkavat kertautumaan. Neljä pyöräytystä riittää tuomaan edun selkeämmin esiin. Mitä pidempään tästä jatkat, sen varmemmin jäät häviölle.
Jos päätät panostaa 10 € neljä kertaa peräkkäin mustalle/punaiselle, käy seuraavasti:
- 29,2 % kerroista jäät voitolle, eli arvaat oikein kolme tai kaikki neljä kierrosta (..jolloin pelaaminen mahdollisesti jatkuu..?)
- 70,8 % kerroista et jää voitolle (..jolloin pelaaminen usein jatkuu.)
- 37,4 % kerroista jäät omillesi, eli arvaat oikein kahdella kierroksella
- 33,4 % kerroista jäät häviölle, eli arvaat oikein kerran tai et kertaakaan
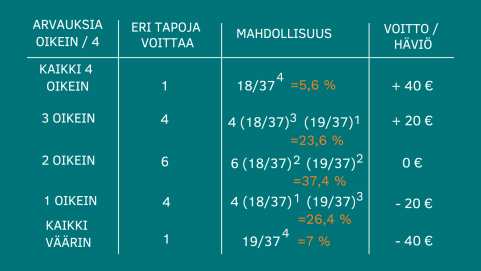
Lähde: Mazur: What’s luck got to do with it? The history, Mathematics and Psychology of the Gambler’s Illusion, s. 103
Katso myös
Hedelmäpelien painotettu tulosarvonta -Läheltä piti -tilanteen harha
Rahapeliautomaatin palautusprosentti - Mistä todella on kysymys?
Satunnaisuus ja tapahtumien riippumattomuus – Voitto on vain sattumaa
Rahapelaamisen matematiikasta -Faktoja satunnaisuudesta, palautusprosentista ja talon edusta
Bonusten matematiikkaa - Onko bonusraha ilmaista rahaa?
Palautusprosentti ja kerroin vedonlyönnissä – Haasta ajatuksesi!